Integrate Fire
This subdirectory contains several simulations that illustrate the capacity of SNNAP to simulate networks containing both Hodgkin-Huxley-type neurons and integrate-and-fire type cells. In addition, the simulations illustrate the different ‘learning rules’ that govern the weights of ‘synapses’ among integrate-and-fire cells.
WS1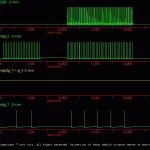
The goal of the present simulation is to illustrate how to implement a hybrid neural network that contains both Hodgkin-Huxley (HH) type neurons and Integrate-and-Fire (gi) cells. In addition, this simulation illustrates the function of *.ws equation 1.
The structure of the network is illustrated in ws1_ntw.jpg. Note that HH and gi types of cells are depicted using different symbols. In addition, weighted synapses (ws) are depicted as open boxes. (Note, modulatory synapses are depicted filled boxes and chemical synapses as open triangles.)
Initially, a stimulus is applied to the gi-type cell ‘gi_6’, elicits firing. The rate of firing is controlled by several factors including the “membrane capacitance” of the gi- type cell, the noise level (see \examples\integrate_fire\ws7), the threshold. gi_6, in turn, makes a synaptic connection with gi_7.cell. The gi_6 to gi_7 weighted synapse uses equation 1 of the *.ws file. This equation has no plasticity and the synaptic weight is a constant. The HH-type cell makes a synaptic connection with gi_6 and a treatment that elicits activity in the HH cell ultimately leads to some activity in gi_6 and gi_7.
The results of this simulation are illustrated in ws1_ous.gif
WS2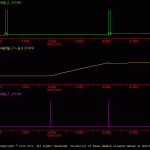
The goals of the present simulation are to illustrate two aspects of neural networks with integrate-and-fire cells and weighted synapses:
Any network must contain at least one HH-type neuron and this neuron must contain at least voltage-dependent conductance with activation and inactivation functions. (see w2_ntw.jpg). SNNAP was originally designed to simulation HH-type neurons and synaptic connections. The present version of SNNAP must ‘see’ at least one HH-type cell. As the integrate-and-fire features of SNNAP are refined, this requirement may be relaxed.
Equation 2, in *.ws. Equation 2 in the *.ws file is referred as ‘associative’ because the voltages of both the pre- and postsynaptic cells are considered in calculating dW/dt (i.e., the change in synaptic weight).
The results of this simulation are illustrated in w2_ous.gif. In this simulation, cell gi_6.cell makes a weighted synaptic connection to gi_7.cell (see w2_ntw.jpg). Two identical stimuli are applied to gi_6.cell, which elicited 2 ‘spikes’ in gi_6.cell. Because the synaptic weight between i_6.cell and gi_7.cell (i.e., weight[gi_7.<-.gi_6..]) this initial activity in gi_6.cell does not elicit a response in gi_7.cell. Before the second stimulus to gi_6.cell, however, a stimulus is applied to gi_7.cell, which elicited activity in gi_7.cell. This activity initiated facilitation of the synaptic connection from gi_6.cell to gi_7.cell (i.e., weight[gi_7.<-.gi_6..]). As a result of this synaptic facilitation, the second stimulus to gi_6.cell elicited a ‘spike’ in the postsynaptic cell.
WS3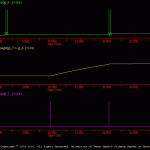
The goal of the present simulation is to illustrate equation 3 of the *.ws file.
Equations 2 and 3 are similar in that both use the ‘voltage’ of the pre- and postsynaptic cells in calculating changes in synaptic weight. The methods used to calculate the rate of change (i.e., dW/dt) are slightly different, however (see User’s Manual or *.ws file). The results of the present simulation are illustrated in w3_ous.gif.
WS4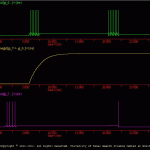
The goal of the present simulation is to illustrate equation 4 of the *.ws file.
Equation 4 (and 5) of the *.ws file are referred to as ‘nonassociative’ in that only the ‘voltage’ of the presynaptic cell is used to determine changes in synaptic weight. Equation 4 induces a long-term potentiation of the synaptic connection, whereas, equation 5 induces synaptic depression.
In this simulation, an initial stimulus is given to the postsynaptic cell (gi_7.cell). This stimulus evokes activity in gi_7.cell, but does not alter the weight of the gi_6 to gi_7 synapse. Subsequently, two stimuli are given to gi6_6.cell (i.e., the presynaptic cell). The first stimulus failed to elicit activity in the postsynaptic cell (i.e., gi_7.cell), but did initiate a nonassociative increase in the synaptic weight. Thus, the second stimulus to the presynaptic cell, which occurred in the presence of enhanced synaptic weight, was able to elicit a postsynaptic response (i.e., a ‘spike’ in gi_7.cell).
Note that the change in synaptic weight reaches an asymptote (i.e., the Wmax parameter in the *.ws file.).
WS5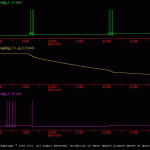
The goal of the present simulation is to illustrate equation 5 of the *.ws file.
Equation 5 is a ‘nonassociative’ learning rule that changes in synaptic weight (i.e., weight[gi_7.<-.gi_6..]) depend only on the ‘voltage’ of the presynaptic cell. Eq. 5 implements long-term depression of a synaptic connection.
As in a previous simulation (\examples\integrate_file\ws4\ws4.smu), an initial stimulus was delivered to the postsynaptic cell (i.e., gi_7.cell). This initial stimulus elicited activity in gi_7.cell, but did not alter the synaptic weight. In addition, two stimuli were given to the presynaptic cell (i.e., gi_6.cell). The first of these presynaptic stimuli evoked a response (i.e., a ‘spike’) in the postsynaptic cell and initiated a depression of the synaptic weight. Thus, a second stimulus to the presynaptic failed to evoke a postsynaptic ‘spike’. The results of this simulation are illustrated in ws5_ous.gif.
WS7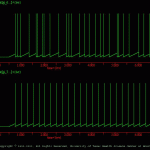
The goal of this simulation is to illustrate how to incorporate noise in the firing pattern of Integrate-and-Fire cells.
For Hodgkin-Huxley type neurons and synaptic connections, noise is introduced via the *.R file. In the Integrate-and-Fire cells, however, noise is incorporated directly into the *.cell file and alter the threshold for firing.
In this example, two identical cells (gi_6.cell and gi_7.cell) receive identical stimuli (a depolarizing current injected between 0.5 and 6.5 seconds). The only difference between the two cells is that noise was incorporated in the threshold of gi_6.cell. Note that the firing pattern of gi_7.cell is very constant, whereas there is variability in the firing pattern of gi_6.cell (see w7_ous.gif). Moreover, as the user runs the simulation over and over again, the pattern of activity in gi_6.cell will vary with each simulation.